Topological Sort Algorithm in Python

Directed Acyclic Graph

A directed acyclic graph is a directed graph that has no cycles. Each edge of the graph is unidirectional. A vertex V4 of a directed graph is said to be reachable from another vertex V1 when there exists a path that starts at V1 and ends at V4.

Topological Sort Algorithm

Topological sort algorithm for Directed Acyclic Graph (DAG) is a linear arrangement of vertices such that for every directed edge x-y, vertex x comes before y in the arrangement. Topological sorting is only applicable on graphs that are DAG.

Topological Sort is given actions in such a way that if there is a dependency of one action on another, then the dependent action always comes later than its parent action.

If the graph is cyclic, topological sort is not defined. We can’t topologically sort an undirected graph either since each edge in an undirected graph creates a cycle. So topological sorts only apply to directed, acyclic graphs(DAG).

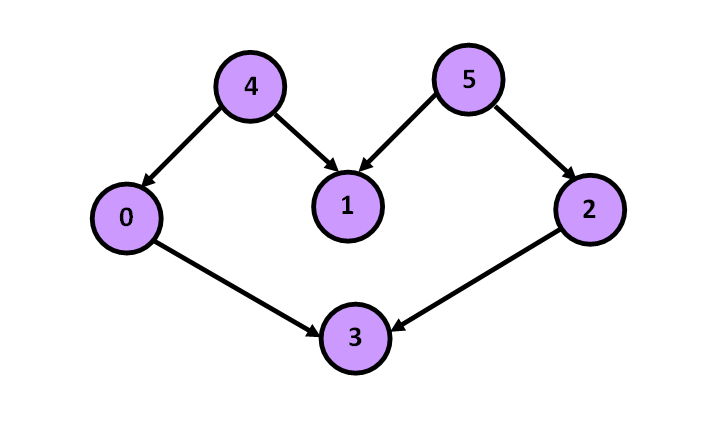
For example, a topological sorting of the given graph is “4, 5, 0, 3, 2, 1”. There can exist more than one topological sorting for a given graph. Another topological sorting for the given example can be “5, 4, 0, 3, 2, 1”. The first vertex in a topological sorting is always a vertex with no incoming edges.

Creation of Graph

To implement the Graph data structure, we first initialize the “Graph” class. Then, we overwrite the __init__ function and create another function to add edges between the newly added nodes.

#Initializing the Graph Class
class Graph:
    def __init__(self, numberofVertices):
        self.graph = defaultdict(list)
        self.numberofVertices = numberofVertices
    
    def addEdge(self, vertex, edge):
        self.graph[vertex].append(edge)

Implementation of Topological Sort Algorithm

For the implementation of the Topological Sort Algorithm in Python, we define two functions – the topologicalSort function for sorting and the topogologicalSortUtil for holding the stack of visited nodes of the graph.

Topological Sort Algorithm is based on the following steps:

• Identify vertices that have no incoming edges.
• Delete this vertex of in-degree 0 and all its outgoing edges from the graph. Place it in the ouput.
• Repeat the steps until the graph is completely empty.

#Implementing Topological Sort
def topogologicalSortUtil(self, v, visited, stack):
    visited.append(v)

    for i in self.graph[v]:
        if i not in visited:
            self.topogologicalSortUtil(i, visited, stack)
        
    stack.insert(0, v)
    
def topologicalSort(self):
    visited = []
    stack = []

    for k in list(self.graph):
        if k not in visited:
            self.topogologicalSortUtil(k, visited, stack)
        
    print(stack)

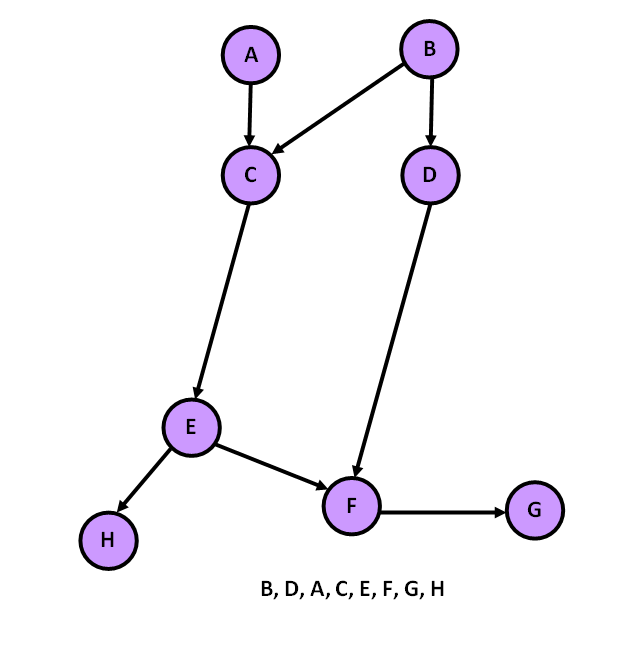
tempGraph = Graph(8)
tempGraph.addEdge("A", "C")
tempGraph.addEdge("C", "E")
tempGraph.addEdge("E", "H")
tempGraph.addEdge("E", "F")
tempGraph.addEdge("F", "G")
tempGraph.addEdge("B", "D")
tempGraph.addEdge("B", "C")
tempGraph.addEdge("D", "F")

tempGraph.topologicalSort()

#Output
['B', 'D', 'A', 'C', 'E', 'F', 'G', 'H']

Time and Space Complexity for Topological Sort

The time complexity for the Topological Sort Algorithm is O(V+E) where “V” and “E” are the numbers of vertices and edges of the graph respectively. We need to traverse all nodes of the graph for implementation. The space complexity is O(V+E) because an additional stack memory is required to store temporary data.