Minimum Spanning Tree in Python

A spanning tree is a subset of a Graph, which has all the vertices covered using a minimum possible number of edges. A spanning tree comprises all the vertices of a given graph. Hence, the graph under consideration must be connected.

A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph which:

• Connects all vertices together
• Has no in-graph cycle
• Holds minimum total edge weight

Hence, a minimum spanning tree is a spanning tree whose sum of edge weights is as small as possible.

The minimum spanning tree finds applications in various real-life problems such as telephone wiring, cancer imaging, astronomy, etc. For example, the following problem can be solved with the knowledge and implementation of the minimum spanning tree data structure:

• Five islands are connected with bridges.
• The cost of bridges between various islands varies based on different factors.
• Construct a bridge to connect all the islands simultaneously at the minimum cost.

Disjoint Set in Python

A disjoint set is a data structure in python that keeps track of a set of elements that are partitioned into a number of disjoint and non-overlapping sets. Each of these sets has representatives that help in identifying those sets. There are three primary operations that can be performed on the disjoint set data structure:

• makeSet(N) – The makeSet function is used to create an initial data sets. It takes the vertices of the given data sets as its parameters.
• union(A,B) – The union method is used to merge two data sets. It takes the two sets to be merged as its parameters.
• findSet(X) – The findSet method is used to check whether a given data set exists or not in the disjoint set data structure. The set to be found is entered as parameter. It returns the set name in which the element is present.

Implementation of Disjoint Set Data Structure

To implement the disjoint set data structure, we first create the DisjointSet class and overwrite the __init__ function. The init function contains two variables – vertices and a dictionary called parent.

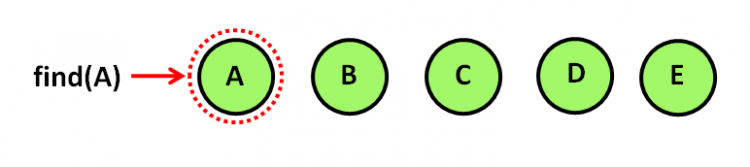
The find function takes the value to be searched as a parameter. If the value is found in the disjoint set, the function returns the same.

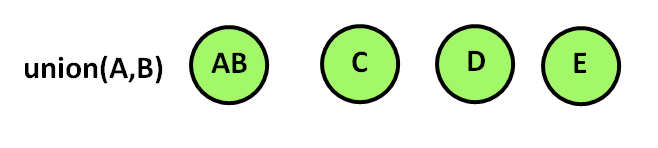
The union method takes two set elements as parameters. It then merges the two data sets based on the order in which they are passed as arguments.

#Implementing Disjoint Set data structure and its functions
class DisjointSet:
    def __init__(self, vertices):
        self.vertices = vertices
        self.parent = {}
        for v in vertices:
            self.parent[v] = v
        self.rank = dict.fromkeys(vertices, 0)
    
    def find(self, item):
        if self.parent[item] == item:
            return item
        else:
            return self.find(self.parent[item])
    
    def union(self, x, y):
        xroot = self.find(x)
        yroot = self.find(y)
        if self.rank[xroot] < self.rank[yroot]:
            self.parent[xroot] = yroot
        elif self.rank[xroot] > self.rank[yroot]:
            self.parent[yroot] = xroot
        else:
            self.parent[yroot] = xroot
            self.rank[xroot] += 1

vertices = ["A", "B", "C", "D", "E"]

ds = DisjointSet(vertices)
ds.union("A", "B")
ds.union("A", "C")
print(ds.find("A"))

#Output
A