Kruskal and Prim’s Algorithm in Python

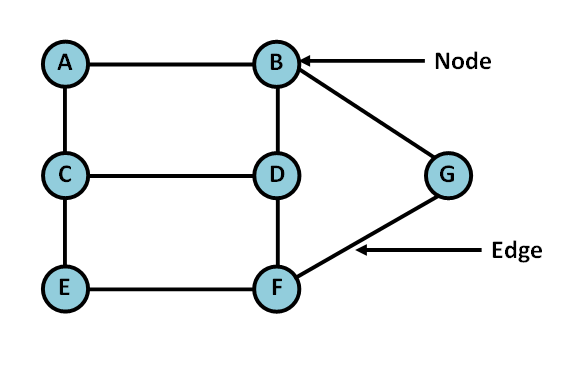
Kruskal’s Algorithm and Prim’s Algorithm are “minimum spanning tree” algorithms. For the implementation of these algorithms, we must have adequate knowledge of Graphs and Disjoint set data structures. Hence, before moving on to the algorithms, we define the necessary data structures.

Creation of Graph

To implement the Graph data structure, we first initialize the “Graph” class. Then, we overwrite the __init__ function and create another function to add weighted edges between the newly added nodes.

#Initializing the Graph Class
class Graph:
    def __init__(self, vertices):
        self.V = vertices
        self.graph = []
        self.nodes = []
        self.MST = []

    def addEdge(self, s, d, w):
        self.graph.append([s, d, w])
    
    def addNode(self, value):
        self.nodes.append(value)

    def printSolution(self,s,d,w):
        for s, d, w in self.MST:
            print("%s - %s: %s" % (s, d, w))

Creation of Disjoint Set

To implement the disjoint set data structure, we first create the DisjointSet class and overwrite the __init__ function. The init function contains two variables – vertices and a dictionary called parent.

The find function takes the value to be searched as a parameter. If the value is found in the disjoint set, the function returns the same.

The union method takes two set elements as parameters. It then merges the two data sets based on the order in which they are passed as arguments.

#Implementing Disjoint Set data structure and its functions
class DisjointSet:
    def __init__(self, vertices):
        self.vertices = vertices
        self.parent = {}
        for v in vertices:
            self.parent[v] = v
        self.rank = dict.fromkeys(vertices, 0)
    
    def find(self, item):
        if self.parent[item] == item:
            return item
        else:
            return self.find(self.parent[item])
    
    def union(self, x, y):
        xroot = self.find(x)
        yroot = self.find(y)
        if self.rank[xroot] < self.rank[yroot]:
            self.parent[xroot] = yroot
        elif self.rank[xroot] > self.rank[yroot]:
            self.parent[yroot] = xroot
        else:
            self.parent[yroot] = xroot
            self.rank[xroot] += 1

Kruskal’s Algorithm in Python

Kruskal’s algorithm is a minimum spanning tree algorithm that takes a graph as input and creates a minimum spanning tree from the subset of that graph. It finds a minimum spanning tree for the weighted undirected graph in the following two ways:

• Add edges in ascending order of weight at each step.
• Avoid any cycle formation at each step.

Implementation of Kruskal’s Algorithm

The implementation of Kruskal’s algorithm is based on the following steps:

• Sort all the edges of the graph from low weight to high.
• Take the edge of the lowest weight and add it to the required spanning tree. If adding this edge creates a cycle in the graph, then reject this edge.
• Repeat this process until all the vertices are covered with the edges.

#Function to implement Kruskal's Algorithm
def kruskalAlgo(self):
    i, e = 0, 0
    ds = dst.DisjointSet(self.nodes)
    self.graph = sorted(self.graph, key=lambda item: item[2])
    while e < self.V - 1:
        s, d, w = self.graph[i]
        i += 1
        x = ds.find(s)
        y = ds.find(d)
        if x != y:
            e += 1
            self.MST.append([s,d,w])
            ds.union(x,y)
    self.printSolution(s,d,w)

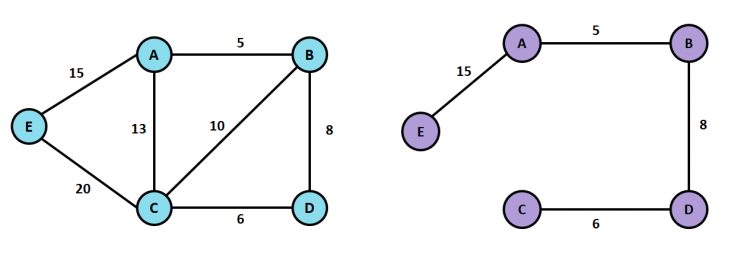
g = Graph(5)
g.addNode("A")
g.addNode("B")
g.addNode("C")
g.addNode("D")
g.addNode("E")
g.addEdge("A", "B", 5)
g.addEdge("A", "C", 13)
g.addEdge("A", "E", 15)
g.addEdge("B", "A", 5)
g.addEdge("B", "C", 10)
g.addEdge("B", "D", 8)
g.addEdge("C", "A", 13)
g.addEdge("C", "B", 10)
g.addEdge("C", "E", 20)
g.addEdge("C", "D", 6)
g.addEdge("D", "B", 8)
g.addEdge("D", "C", 6)
g.addEdge("E", "A", 15)
g.addEdge("E", "C", 20)

g.kruskalAlgo()

Output

Time and Space Complexity

The time complexity for Kruskal’s algorithm is O(V + ElogE + EV) where “V” is the number of vertices and “E” is the number of edges in the graph. The space complexity is O(V+E) as we need additional memory to store data elements temporarily.

Prim’s Algorithm in Python

Prim’s algorithm is a minimum spanning tree algorithm that takes a graph as input and creates a minimum spanning tree from the subset of that graph. It finds a minimum spanning tree for the given weighted undirected graph.

Implementation of Prim’s Algorithm

The implementation of Prim’s algorithm is based on the following steps:

• Take any vertex as the source and set its weight to 0. Set the weights of all other vertices to infinity.
• For every adjacent vertices, if the current weight is more than that of the current edge, then we replace it with the weight of the current edge.
• Then, we mark the current vertex as visited.
• Repeat these steps for all the given vertices in ascending order of weight.

#Function to implement Prim's Algorithm
def primsAlgo(self):
    visited = [0]*self.vertexNum
    edgeNum=0
    visited[0]=True
    while edgeNum<self.vertexNum-1:
        min = sys.maxsize
        for i in range(self.vertexNum):
            if visited[i]:
                for j in range(self.vertexNum):
                    if ((not visited[j]) and self.edges[i][j]):
                        if min > self.edges[i][j]:
                            min = self.edges[i][j]
                            s = i
                            d = j
        self.MST.append([self.nodes[s], self.nodes[d], self.edges[s][d]])
        visited[d] = True
        edgeNum += 1
    self.printSolution()

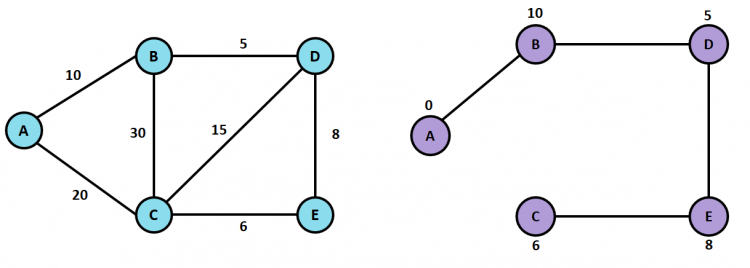
edges = [[0, 10, 20, 0, 0],
		[10, 0, 30, 5, 0],
		[20, 30, 0, 15, 6],
		[0, 5, 15, 0, 8],
		[0, 0, 6, 8, 0]]

nodes = ["A","B","C","D","E"]
g = Graph(5, edges, nodes)
g.primsAlgo()

Output

Time and Space Complexity

The time complexity for Prim’s algorithm is O(V^3) as we use three nested loops, each iterating over the vertices of the graph. The space complexity is O(V) as we need additional memory to store data elements temporarily.

Kruskal vs Prim’s Algorithm

Kruskal’s Algorithm	Prim’s Algorithm
Kruskal’s algorithm concentrates on edges.	Prim’s algorithm concentrates on vertices.
Finalizes 1 edge in each iteration.	Finalizes 1 vertex edge in each iteration.
Applications – Landing Cables – TV Network – Tour Operations – LAN Network	Applications – Cluster Analysis -Travelling Salesman Problem – Network for roads and rail tracks – Designing fiber optics grid