Binary Search Tree in Python

A Binary Search Tree is a Binary Tree data structure in which nodes are arranged in a specific order. A binary search tree satisfies the following properties:

• The left subtree of a node contains only nodes with values lesser than the node’s value.
• The right subtree of a node contains only nodes with values greater than the node’s value.
• The left and right subtree of each node must also be a binary search tree.

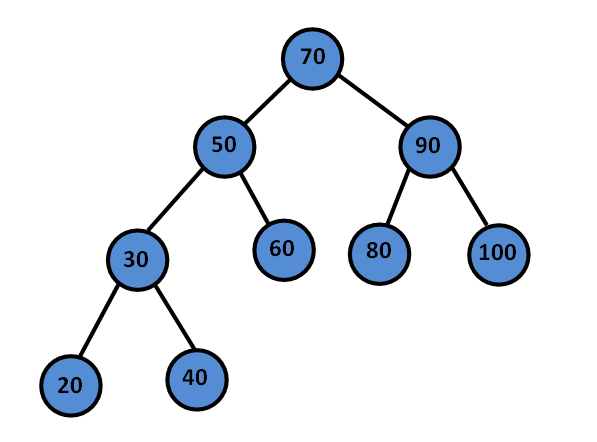
In a Binary Search Tree, the elements are arranged in an ordered/sorted manner in contrast to a normal binary tree. This efficiently reduces the amount of time it takes to perform certain operations such as searching, insertion, and deletion.

Creation of Binary Search Tree

To initialize a binary search tree, we create a Binary Search tree class having three components – a data value, reference to the left child node, and reference to the right child node. While implementing the various operations of a binary search tree, we will use the queue data structure built using a linked list.

We have dedicated an article for queue built using a linked list. For a detailed explanation of the Queue class below, refer to that article.

#Creating the Queue class using linked list
class Node:
    def __init__(self, value=None):
        self.value = value
        self.next = None

    def __str__(self):
        return str(self.value)


class LinkedList:
    def __init__(self):
        self.head = None
        self.tail = None

    def __iter__(self):
        node = self.head
        while node:
            yield node
            node = node.next

class Queue:
    def __init__(self):
        self.linkedList = LinkedList()

    def __str__(self):
        values = [str(x) for x in self.linkedList]
        return ' '.join(values)

    def enqueue(self, value):
        new_node = Node(value)
        if self.linkedList.head == None:
            self.linkedList.head = new_node
            self.linkedList.tail = new_node
        else:
            self.linkedList.tail.next = new_node
            self.linkedList.tail = new_node

    def isEmpty(self):
        if self.linkedList.head == None:
            return True
        else:
            return False

    def dequeue(self):
        if self.isEmpty():
            return "The Queue is empty."
        else:
            tempNode = self.linkedList.head
            if self.linkedList.head == self.linkedList.tail:
                self.linkedList.head = None
                self.linkedList.tail = None
            else:
                self.linkedList.head = self.linkedList.head.next
            return tempNode

    def peek(self):
        if self.isEmpty():
            return "The Queue is empty."
        else:
            return self.linkedList.head

    def delete(self):
        self.linkedList.head = None
        self.linkedList.tail = None

#Creating the Binary Search Tree Class
import QueueLinkedList as queue

class BSTNode:
    def __init__(self, data):
        self.data = data
        self.leftChild = None
        self.rightChild = None

newTree = BSTNode(None)

Time and Space Complexity

The time complexity for the creation of a binary search tree is O(1) because it takes constant time for the initialization of data variables. The space complexity is O(1) as well since no additional memory is required.

Operations on Binary Search Tree

Insertion in Binary Search Tree

The process of insertion in a binary search tree is ordered. This means that when we are inserting a node in a binary search tree, we must locate the right place where the node must be inserted according to the value it holds.

Example :

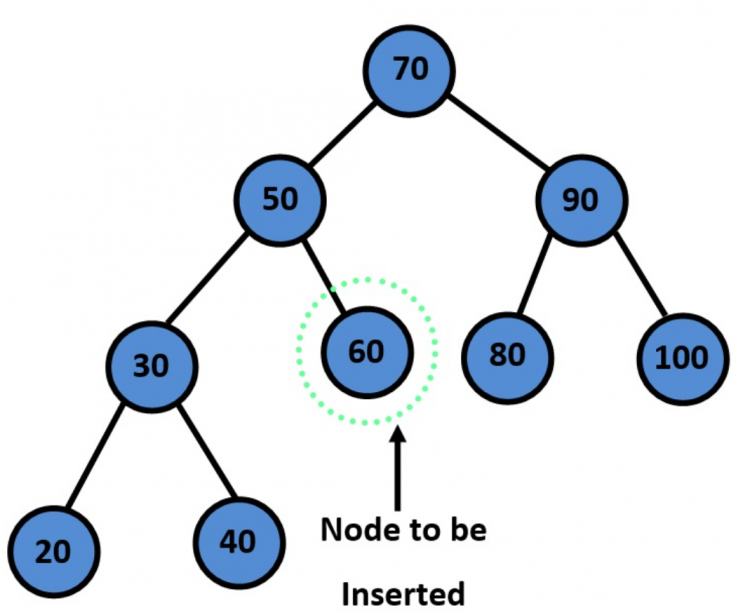
Implementation of Insertion in Binary Search Tree

While insertion, we compare the values of the nodes we visit with the value of the node to be inserted. We can encounter any of the three following situations:

• If the binary tree is empty, insert the new node and set it as the root of the binary search tree.
• If the value of the new node is less than the value of the parent, move to the left subtree and continue the process of comparison until the correct position is found.
• If the value of the new node is greater than the value of the parent, move to the right subtree and continue the process of comparison until the correct position is found.

#Function to insert nodes in Binary Search Tree
def insertNode(root_node, node_value):
    if root_node.data == None:
        root_node.data = node_value
    elif node_value <= root_node.data:
        if root_node.leftChild is None:
            root_node.leftChild = BSTNode(node_value)
        else:
            insertNode(root_node.leftChild, node_value)
    else:
        if root_node.rightChild is None:
            root_node.rightChild = BSTNode(node_value)
        else:
            insertNode(root_node.rightChild, node_value)
    return "The node has been successfully inserted."

#Initializing the Binary Search Tree
newTree = BSTNode(None)
insertNode(newTree, 70)
insertNode(newTree, 50)
insertNode(newTree, 90)
insertNode(newTree, 30)
insertNode(newTree, 80)
insertNode(newTree, 100)
insertNode(newTree, 20)
insertNode(newTree, 40)

print(insertNode(newTree, 60))

#Output
The node has been successfully inserted.

Time and Space Complexity

The recursive function searches for the correct position by dividing the subtrees at each level and moving on to the next level depending on the value of the node. In this way, the number of function calls takes the form of logN. Hence, the time complexity for insertion is O(logN).

The space complexity is O(logN) as well because every time the function is called, it allocates space in the stack in memory to determine the next function call.

Traversal in Binary Search Tree

Traversal is the process of visiting every node in the tree, exactly once, to print values, search nodes, etc. For a Binary Search Tree, traversal can be implemented in any of the following ways:

• Depth First Traversals:
  • Inorder (Left, Root, Right)
  • Preorder (Root, Left, Right)
  • Postorder (Left, Right, Root) 

• Breadth-First Traversal:
  • Level Order Traversal

PreOrder Traversal in Binary Search Tree

Pre-order traversal visits the current node before its child nodes. In a pre-order traversal, the root is always the first node visited.

Example:

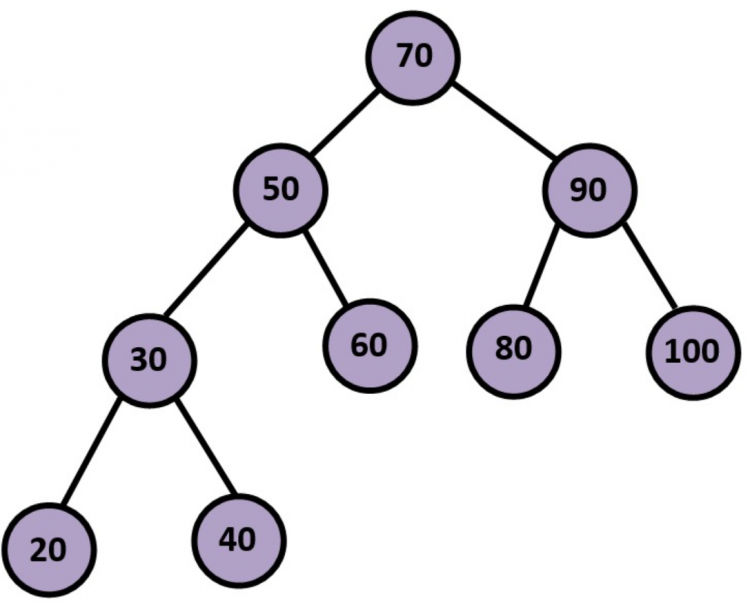
PreOrder Traversal – 70 -> 50 -> 30 -> 20 -> 40 -> 60 -> 90 -> 80 -> 100

Implementation of PreOrder Traversal in Binary Search Tree

For implementing pre-order traversal in a binary search tree, the below code makes use of a recursive function preOrderTraversal. Initially, the root node is passed as an argument to this function.

If the root node is not empty, its content is displayed followed by calling the same recursive function with the left and right of the current node. The function preOrderTraversal terminates a recursion when the encountered node is found to be empty.

#Function to implement PreOrder Traversal
def preOrderTraversal(root_node):
    if not root_node:
        return
    print(root_node.data)
    preOrderTraversal(root_node.leftChild)
    preOrderTraversal(root_node.rightChild)

#Initializing the Binary Search Tree
newTree = BSTNode(None)
insertNode(newTree, 70)
insertNode(newTree, 50)
insertNode(newTree, 90)
insertNode(newTree, 30)
insertNode(newTree, 80)
insertNode(newTree, 100)
insertNode(newTree, 20)
insertNode(newTree, 40)

preOrderTraversal(newTree)

Output

Time and Space Complexity

The time complexity for PreOrder traversal is O(N) because the function recursively visits all nodes of the tree. When we use a recursive function, it holds up memory in the stack so as to recognize its next call. Thus, the space complexity for PreOrder traversal is O(N).

InOrder Traversal in Binary Search Tree

In-order traversal means to visit the left branch, then the current node, and finally, the right branch.

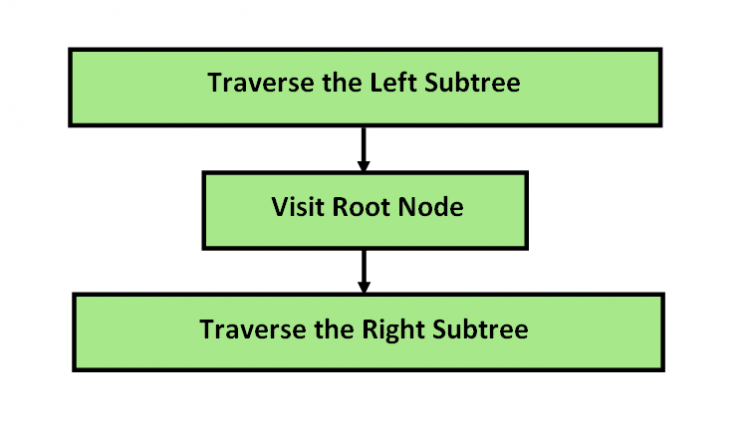
Example:

InOrder Traversal – 20 -> 30 -> 40 -> 50 -> 60 -> 70 -> 80 -> 90 -> 100

Implementation of InOrder Traversal in Binary Search Tree

For implementing in-order traversal in a binary search tree, the below code makes use of a recursive function inOrderTraversal. Initially, the root node is passed as an argument to this function.

If the root node is not empty, a recursive call to the left child is made, followed by displaying the content of the current node, and then a recursive call to the right child is made. The function inOrderTraversal terminates a recursion when the encountered node is found to be empty.

#Function to implement InOrder Traversal
def inOrderTraversal(root_node):
    if not root_node:
        return
    inOrderTraversal(root_node.leftChild)
    print(root_node.data)
    inOrderTraversal(root_node.rightChild)

#Initializing the Binary Search Tree
newTree = BSTNode(None)
insertNode(newTree, 70)
insertNode(newTree, 50)
insertNode(newTree, 90)
insertNode(newTree, 30)
insertNode(newTree, 80)
insertNode(newTree, 100)
insertNode(newTree, 20)
insertNode(newTree, 40)

inOrderTraversal(newTree)

Output

Time and Space Complexity

The time complexity for InOrder traversal is O(N) because the function recursively visits all nodes of the tree. The space complexity for InOrder traversal is O(N) because the stack holds memory continuously while using a recursive function.

PostOrder Traversal in Binary Search Tree

Post-order traversal means visiting the left branch, then the current node, and finally, the right branch. In a post-order traversal, the root is always the last node visited.

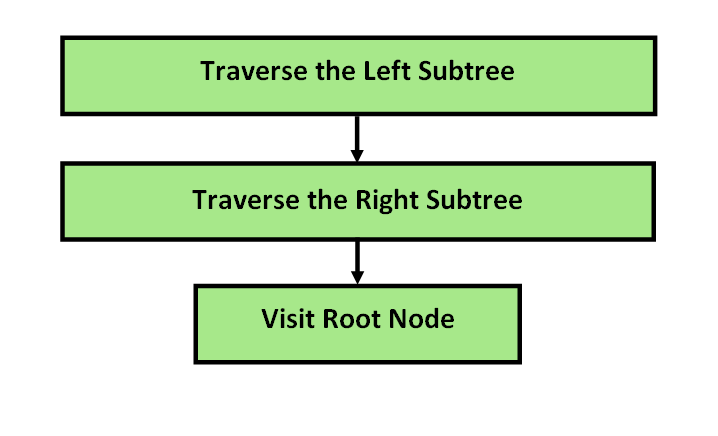
Example:

PreOrder Traversal – 20 -> 40 -> 30-> 60 -> 50 -> 80 -> 100 -> 90 -> 70

Implementation of PostOrder Traversal in Binary Search Tree

For implementing in-order traversal in a binary search tree, the below code makes use of a recursive function postOrderTraversal. Initially, the root node is passed as an argument to this function.

If the root node is not empty, a recursive call to the left child is made, followed by a recursive call to the right child, and then a displaying the content of the current node. The function postOrderTraversal terminates a recursion when the encountered node is found to be empty.

#Function to implement PostOrder Traversal
def postOrderTraversal(root_node):
    if not root_node:
        return
    postOrderTraversal(root_node.leftChild)
    postOrderTraversal(root_node.rightChild)
    print(root_node.data)

#Initializing the Binary Search Tree
newTree = BSTNode(None)
insertNode(newTree, 70)
insertNode(newTree, 50)
insertNode(newTree, 90)
insertNode(newTree, 30)
insertNode(newTree, 80)
insertNode(newTree, 100)
insertNode(newTree, 20)
insertNode(newTree, 40)

postOrderTraversal(newTree)

Output

Time and Space Complexity

The time complexity for PostOrder traversal is O(N) because the function recursively visits all nodes of the tree. The space complexity for PostOrder traversal is O(N) because the stack holds memory continuously while using a recursive function.

Level Order Traversal in Binary Search Tree

Trees can also be traversed in a level order manner. The Level Order traversal is a breadth-first traversal where nodes are visited level-by-level. Then, they are traversed in a left-to-right manner.

Example:

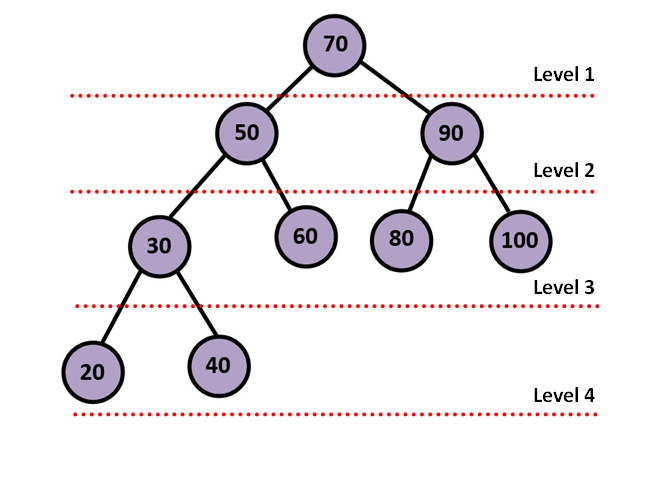
Level Order Traversal – 70 -> 50 -> 90 -> 30 -> 60 -> 80 -> 100 -> 20 -> 40

Implementation of Level Order Traversal in Binary Search Tree

For implementing level-order traversal in a binary search tree, the below code makes use of a queue to implement the same. The function levelOrderTraversal is initially called with the root node as its parameter.

If the current node is not empty, the same is pushed into a queue, followed by iterating the queue. Queue iteration works as follows:

• The first element is dequeued and its content is displayed.
• The children of this node are enqueued into the same queue.
• The same procedure is implemented for all nodes that enter the queue.
• The function terminates when every element is dequeued.

#Function to implement LevelOrder Traversal
def levelOrderTraversal(root_node):
    if not root_node:
        return
    else:
        customQueue = queue.Queue()
        customQueue.enqueue(root_node)
        while not(customQueue.isEmpty()):
            root = customQueue.dequeue()
            print(root.value.data)
            if root.value.leftChild is not None:
                customQueue.enqueue(root.value.leftChild)
            if root.value.rightChild is not None:
                customQueue.enqueue(root.value.rightChild)

#Initializing the Binary Search Tree
newTree = BSTNode(None)
insertNode(newTree, 70)
insertNode(newTree, 50)
insertNode(newTree, 90)
insertNode(newTree, 30)
insertNode(newTree, 80)
insertNode(newTree, 100)
insertNode(newTree, 20)
insertNode(newTree, 40)

levelOrderTraversal(newTree)

Output

Time and space Complexity

The time complexity for Level Order traversal is O(N) because the function visits all nodes of the tree. The space complexity for Level Order traversal is O(N) because we store the data of the tree in a temporary queue.

Searching for a node in Binary Search Tree

In a Binary Search Tree, the left child of a node has a value lesser than that node and the right child has a greater value. Thus, while searching, we compare the value to be searched with that of the node we visit.

If the value is less than that of the node, we traverse the left subtree. Otherwise, we traverse the right subtree. This optimizes the time utilization as we divide the tree at each level during our search.

Example:

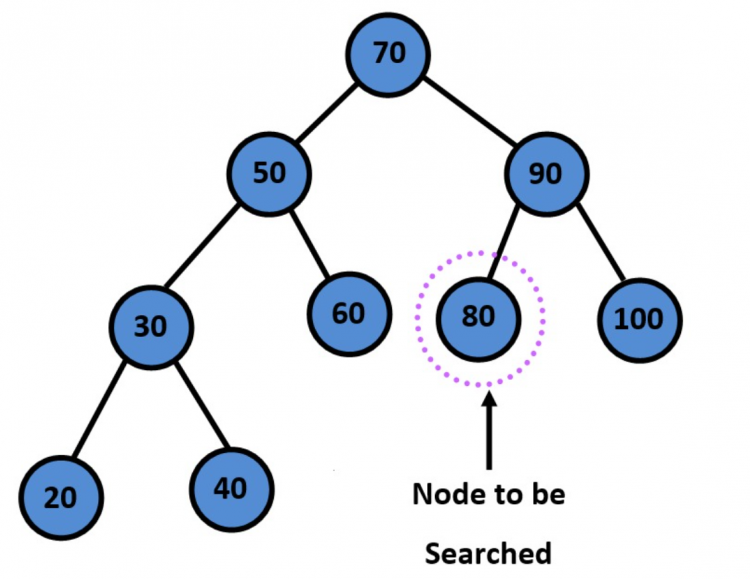
Implementation of Search in Binary Search Tree

To implement searching a node in a binary search tree, we create a function searchNode that takes two arguments -the root node of the tree and the value to be searched.

The recursive function compares the value of the current node with the value to be searched. Further, the recursive function is called for the left child or the right child of the current node depending on whether the value to be searched is lesser or greater than the current node.

#Searching a node in a Binary Search Tree
def searchNode(root_node, node_value):
    if root_node.data == node_value:
        print("The element has been found.")
    elif node_value < root_node.data:
        if root_node.leftChild.data == node_value:
            print("The element has been found.")
        else:
            searchNode(root_node.leftChild, node_value)
    else:
        if root_node.rightChild.data == node_value:
            print("The element has been found.")
        else:
            searchNode(root_node.rightChild, node_value)

#Initializing the Binary Search Tree
newTree = BSTNode(None)
insertNode(newTree, 70)
insertNode(newTree, 50)
insertNode(newTree, 90)
insertNode(newTree, 30)
insertNode(newTree, 80)
insertNode(newTree, 100)
insertNode(newTree, 20)
insertNode(newTree, 40)

searchNode(newTree, 90)

#Output
The element has been found.

Time and space Complexity

The recursive function searches for the correct node by dividing the subtrees at each level and moving on to the next level depending on the value of the node. In this way, the number of function calls takes the form of logN. Hence, the time complexity for search is O(logN).

The space complexity is O(logN) as well because every time the function is called, it allocates space in the stack in memory to determine the next function call.

Deleting a node from Binary Search Tree

While deletion in a binary search tree, we can encounter any of the following three cases:

• The node to be deleted is a leaf node.
• The node to be deleted has a child node.
• The node to be deleted has two children.

Example:

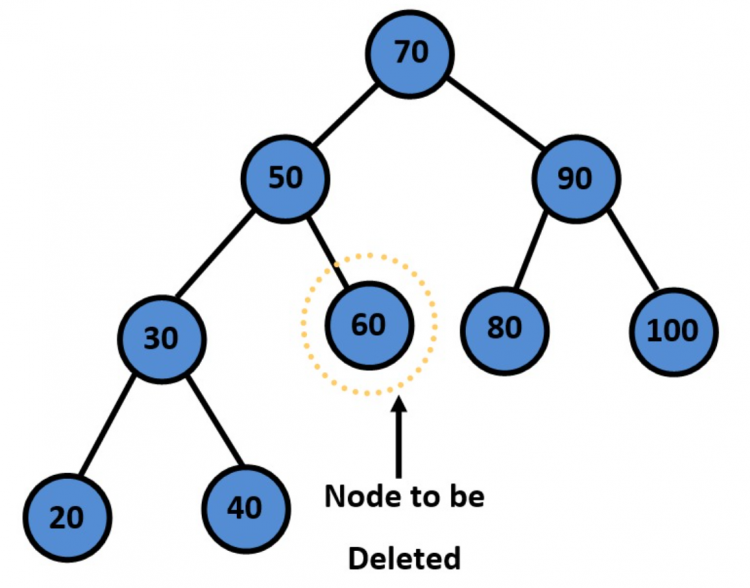
After Deletion:

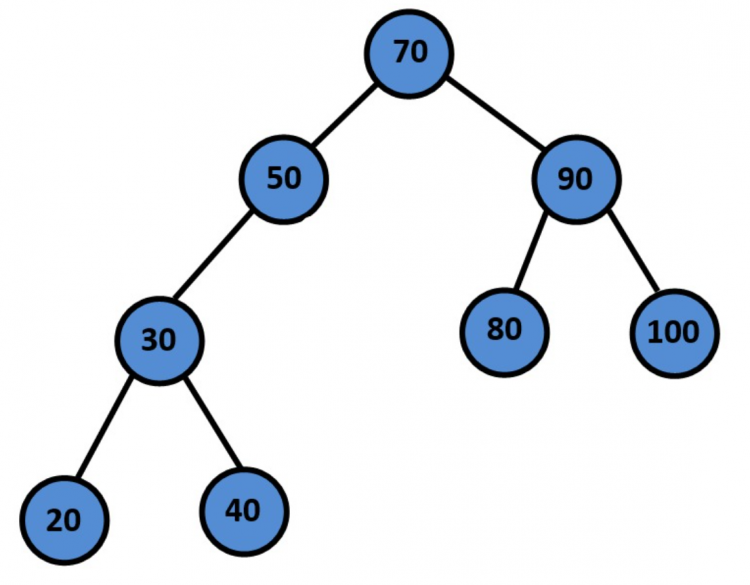
Implementation of Delete in Binary Search Tree

• The node to be deleted is a leaf node: We simply remove the node.
• The node to be deleted has a child node: Copy the child to the node and delete the child.
• The node to be deleted has two children: We find the minimum value in the right subtree of current node using the minValueNode function and replace it with the current node to be deleted.

#Deleting a node from a Binary Search Tree
def minValueNode(bstNode):
    current = bstNode
    while (current.leftChild is not None):
        current = current.leftChild
    return current

def deleteNode(root_node, node_value):
    if root_node is None:
        return root_node
    if node_value < root_node.data:
        root_node.leftChild = deleteNode(root_node.leftChild, node_value)
    elif node_value > root_node.data:
        root_node.rightChild = deleteNode(root_node.rightChild, node_value)
    else:
        if root_node.leftChild is None:
            temp = root_node.rightChild
            root_node = None
            return temp

        if root_node.rightChild is None:
            temp = root_node.leftChild
            root_node = None
            return temp

        temp = minValueNode(root_node.rightChild)
        root_node.data = temp.data
        root_node.rightChild = deleteNode(root_node.rightChild, temp.data)
    return root_node

#Initializing the Binary Search Tree
newTree = BSTNode(None)
insertNode(newTree, 70)
insertNode(newTree, 50)
insertNode(newTree, 90)
insertNode(newTree, 30)
insertNode(newTree, 80)
insertNode(newTree, 100)
insertNode(newTree, 20)
insertNode(newTree, 40)

deleteNode(newTree, 50)
levelOrderTraversal(newTree)

#Output

Time and space Complexity

The recursive function searches for the node to be deleted by dividing the subtrees at each level and moving on to the next level depending on the value of the node. In this way, the number of function calls takes the form of logN. Hence, the time complexity for search is O(logN).

The space complexity is O(logN) as well because every time the function is called, it allocates space in the stack in memory to determine the next function call.

Clearing of Entire Binary Search Tree

To delete an entire binary search tree, we simply set the root node and left and right child references to None. This way we free up the allocated memory space.

#Function to Delete Entire Binary Search Tree
def deleteBST(root_node):
    root_node.data = None
    root_node.leftChild = None
    root_node.rightChild = None
    return "The Binary Search Tree has been successfully deleted."

#Initializing the Binary Search Tree
newTree = BSTNode(None)
insertNode(newTree, 70)
insertNode(newTree, 50)
insertNode(newTree, 90)
insertNode(newTree, 30)
insertNode(newTree, 80)
insertNode(newTree, 100)
insertNode(newTree, 20)
insertNode(newTree, 40)

print(def deleteBST(root_node))

#Output
The Binary Search Tree has been successfully deleted.

Time and Space Complexity

The time complexity for deletion of the entire binary search tree is O(1) since it takes constant time for setting the references to None. The space complexity is O(1) as well since no additional memory is required for deletion.

Time and Space Complexity of Binary Search Tree

	Time Complexity	Space Complexity
Create BST	O(1)	O(1)
Insert a node BST	O(logN)	O(logN)
Traverse BST	O(N)	O(N)
Search for a node BST	O(logN)	O(logN)
Delete a node from BST	O(logN)	O(logN)
Delete Entire BST	O(1)	O(1)